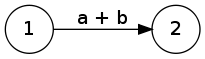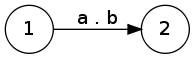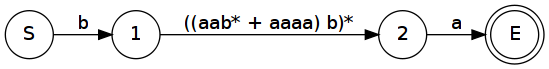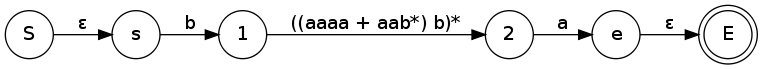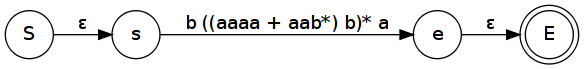Obsah
Regulární jazyky a jejich modely
Jazyk je regulární tehdy, pokud existuje konečný automat, který akceptuje právě všechna slova z jazyka L.
Uzávěrové vlastnosti
Množina uzavřená na operaci – Vezmu dva prvky z množiny (přirozená čísla), provedu s nimi operaci (sečtu je) a výsledek bude zase prvek z té samé množiny (zase přirozené číslo)
Regulární jazyk je uzavřen na skoro všechny operace, ale musí být konečné.
Důkaz, že jazyk je regulární
- Pumping lemma – používá se k dokazování, že daný jazyk NENÍ regulární.
Pojmy
- Prázdné slovo (ε) – Prázdný řetězec, který ale vyhovuje jazyku (je možné jej vygenerovat/přijmout)!
- Řetězec – jakákoli posloupnost terminálních i netereminálních symbolů (znaků)
- Větná forma – řetězec, který lze odvodit z počátečního symbolu gramatiky
- Věta – větná forma pouze z terminálních symbolů
- Jazyk – podmnožina všech řetězců nad abecedou (L ⊆ Σ)
Regulární gramatika
Regulární jazyk je definován regulární gramatikou.
Je to čtveřice:1)
- Konečná množina terminálních symbolů (T, abeceda)
- Konečná množina neterminálních symbolů (N)
- Konečná množina pravidel (P)
- Počáteční symbol (S)
Příklad: G = ({a, b}, {A, B, C}, P, A)
P = {
- A → ε | aB
- B → bC
- C → a
}
Pravidla musí být ve tvaru „neterminál → terminál a neterminál“ nebo „neterminál → terminál“! Vyjímkou je počáteční symbol gramatiky, který může být přepsán na prázdné slovo, ale pak se počáteční symbol nesmí vyskytovat na pravé straně pravidla.
„Odvození“ = použití pravidla (přímé – jedno pravidlo, v k krocích – k pravidel)
Konečné automaty
Je to pětice:
- Neprázdná konečná množina stavů (Q)
- Konečná vstupní abeceda (T)
- Parciální přechodová funkce (δ: Q × T → Q, je možné ji zadat grafem, tabulkou nebo výčtem)
- Počáteční stav (s ∈ Q)
- Množina akceptujících stavů (F ⊆ Q)
Příklad: A = ({q0, q1, q2}, {a, b}, δ, q0, {q0, q2})
- δ(q0, a) = q2
- δ(q1, b) = q1
- δ(q2, a) = q0
- Deterministický – nejvíce jeden přechod pod jedním znakem (u každého stavu)
- Nedetrministický – více přechodů pod jedním znakem
- S ε-kroky – je možné nenačítat další symbol, a přejít ze stavu do stavu pod znakem ε
Automaty jsou ekvivalentní pokud přijímají i zamítají stejná slova.
Může skončit třemi stavy:
- Po přečtení slova skončíme v některém z koncových (akceptujících) stavů – v takovém případě je slovo přijato.
- Po přečtení slova skončíme v jiném než koncovém stavu – slovo je zamítnuto.
- Nedočteme slovo (někde uprostřed slova se dostaneme do stavu, kdy nejsme schopni zpracovat další znak protože neexistuje pro ten znak přechod) – slovo je zamítnuto.
Determinizace
- Pokud má nedeterministický konečný automat n stavů, bude jeho deterministická varianta mít nejvíce 2n stavů.
- Každý nedeterministický konečný automat má svoji deterministickou variantu.
- Deterministický konečný automat nemusí být minimální (a většinou ani není).
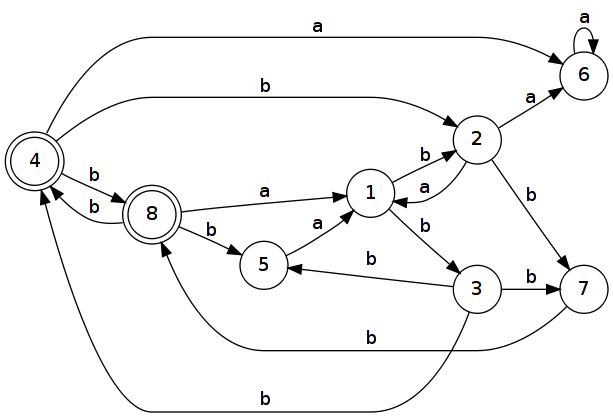
Příklad
- Dostaneme zadaný graf, nebo rovnou tabulku.
- Graf přepíšeme do tabulky.
| a | b | |
|---|---|---|
| →1 | ∅ | {2, 3} |
| 2 | {1, 6} | {7} |
| 3 | ∅ | {4, 5, 7} |
| ←4 | {6} | {2, 8} |
| 5 | {1} | ∅ |
| 6 | {6} | ∅ |
| 7 | ∅ | {8} |
| ←8 | {1} | {4, 5} |
Teď opíšeme první řadek.
| a | b | |
|---|---|---|
| →1 | ∅ | {2, 3} |
V něm je stav {2, 3}, připíšeme ho tedy do tabulky. Pak se podíváme do první tabulky, do jakých stavů se můžeme ze stavů 2 a 3 dostat, pokud příjmeme a nebo b.
| a | b | |
|---|---|---|
| →1 | ∅ | {2, 3} |
| {2, 3} | {1, 6} | {4, 5, 7} |
Teď nám tu přibyly 2 nové stavy ({1, 6} a {4, 5, 7}), uděláme tedy opět to samé co v minulém kroku. Tohle budeme opakovat neustále dokola, dokud nebudeme mít všechny stavy. Pokud je v tom novém stavu nějký stav který byl koncovým (např. 4 v {4, 5, 7}), bude i ten nový stav koncovým.
| a | b | |
|---|---|---|
| →{1} | ∅ | {2, 3} |
| {2, 3} | {1, 6} | {4, 5, 7} |
| {1, 6} | {6} | {2, 3} |
| ←{4, 5, 7} | {1, 6} | {2, 8} |
| {6} | {6} | ∅ |
| ←{2, 8} | {1, 6} | {4, 5, 7} |
Regulární výrazy
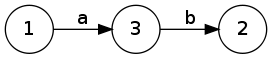
- a . b – konkatenace / zřetězení (jako v PHP)
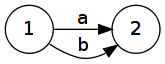
- a + b – nebo, OR
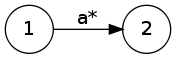
- a*, a+ – iterace (zřetězení)
- L2)(ε) = {ε}
- L(∅) = ∅
- L(a) = {a}
- L(E . F) = L(E) . L(F)
- L(E + F) = L(E) ∪ L(F)
- L(E*) = L(E)*
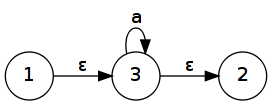
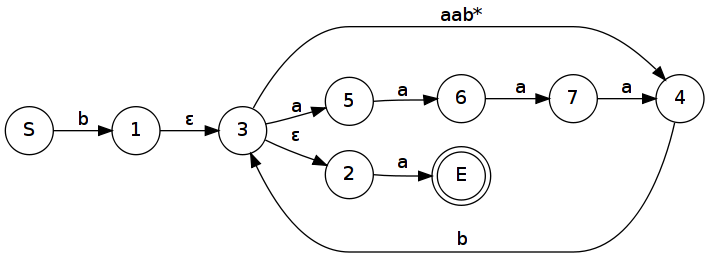
Převod regulárního výrazu na konečný automat
Nejdřív uděláme počáteční a koncový stav a mezi ně na přechod napíšeme regexp. Ten pak postupně (směrem zvenku dovnitř) rozgenerováváme podle následujících pravidel dokud není na každé hraně právě jeden symbol.
Příklad
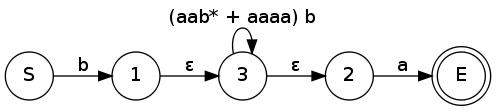
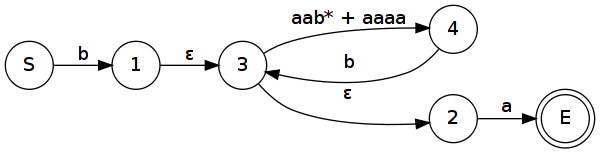
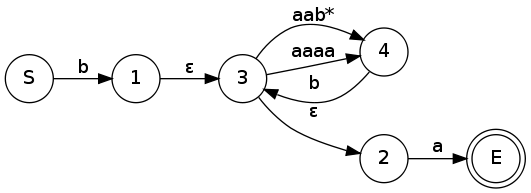
Převod konečného automatu na regulární výraz
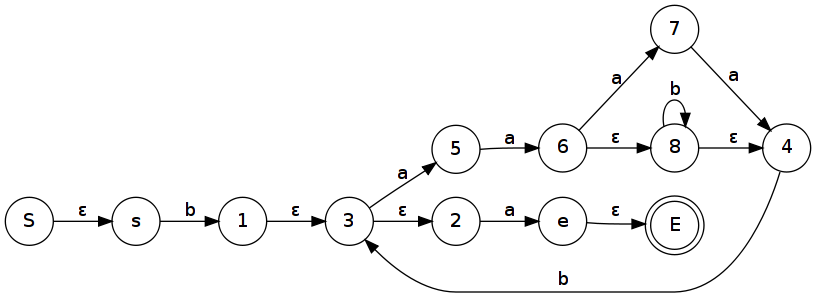
- Automat „obalíme“ novým počátečním a koncovým stavem na které přes ε přechody navážeme ty staré.
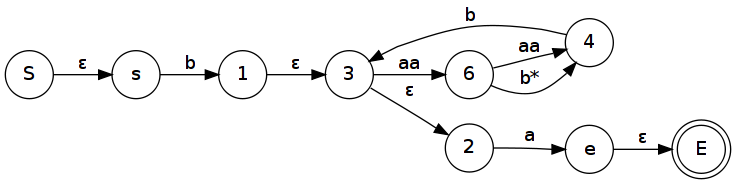
- Pak postupně škrtáme uzly grafu a nahrazujeme je hranami, podle dříve uvedených pravidel, ale v opačném pořadí.
- Opakujeme krok 2 dokud nedostaneme jen počáteční a koncový stav s jednou hranou která představuje regulární výraz.
Příklad
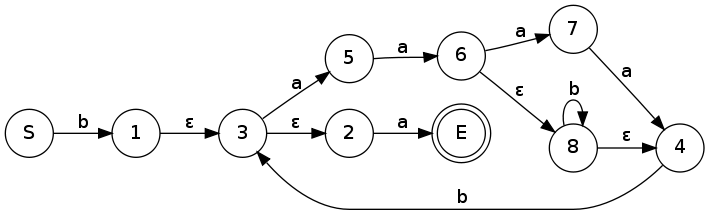
Převedeme minule vytvořený konečný automat zpět na regulární výraz.
Ještě bysme mohli odstranit ε přechody 
Shrnutí
- regulární jazyk: formální jazyk, generován regulární gramatikou, existuje konečný automat, který přijme právě všechna slova z jazyka
- dva modely: konečný automat, regulární výraz
- jeden lze převést na druhý
- regulární gramatika: čtveřice (viz výše), pravidla: neterminál → terminál a neterminál, možno vypustit druhý neterminál, odvození
- konečný automat: pětice (viz výše), determinismus, ekvivalence, umět nakreslit a převést na reg. výraz
- regulární výraz: jiný model regulárního jazyka, lze převést na konečný automat, konkatenace ., zřetězení (+ vs *), „nebo“ +, umět napsat a převést
- lze použít pumping lemmu na dokázání, že jazyk není regulární