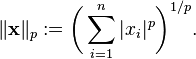Obsah
Matematické struktury v informatice
- Argumentem komplexního čísla je jeho úhel vzhledem k reálné ose. Komplexní číslo má pak tvar r(cosφ + isinφ).
Axiomy
- A → (B → A)
- (A → (B → C)) → ((A → B) → (A → C))
- (¬B → ¬A) → (A → B)
- Modus ponens (pravidlo odloučení) A → B můžeme přepsat na A ⊢ B1).
- Věta o dedukci je Modus ponens obráceně.
- Pravidlo zobecnění znamená, že někam připíšeš ∀x
- Axiom kvantifikátoru – ∀x(A ⇒ B) → (A ⇒ ∀xB)
Struktura = (množina, binární operace)
http://algebra.matfyz.info/1/struktury.jpg, Template:Algebraic structures
| grupoid | uzavřenost |
|---|---|
| pologrupa | asociativita2) |
| monoid | neutrální prvek |
| grupa | inverzní prvek |
Pokud je operace komutativní, je i struktura komutativní („komutativní grupoid“).
Podgrupy
Zmenšíme M, případně upravíme operaci. Musí to ale pořád být grupa (nesmí z M zmizet neutrální a inverzní prvek)!
Struktura = (množina, aditivní operace, multiplikativní operace)
| okruh | (M, +, ·): ((M, +) = komutativní grupa ∧ (M, ·) = monoid ∧ distributivita3) |
|---|---|
| obor integrity | neexistují dělitelé „nuly“ |
| těleso | obor integrity (okruh), kde jsou všechny „nenulové“ prvky invertibilní4) |
| pole | komutativní těleso |
- „Nula“ – neutrální prvek +
- „Jedinčka“ – neutrální prvek ·
- Pokud je (M, ·) komutativní monoid, je i struktura komutativní („komutativní okruh“).
Kongruence
g1 ≡ g2 ∧ h1 ≡ h2 ⇒ g1 ★ h1 ≡ g2 ★ h2
- ★ je libovolná operace ve struktuře
- ≡ znamená kongruence
Pravá kongruence: g1 ≡ g2 ⇒ g1 ★ w ≡ g2 ★ w
Aby to vůbec mohla být kongruence, musí platit relace ekvivalence!
- Reflexivita: a ~ a
- Symetrie: a ~ b ∧ b ~ a
- Tranzitivita: a ~ b ∧ b ~ c ∧ c ~ a
Homomorfizmus
Zobrazení třeba z (ℂ, +) → (ℝ, ⊕).
f(a + b) = f(a) ⊕ f(b)
a, b ∈ ℂ
Když má ta struktura víc operací, musí se dokazovat pro všechny!
Jádro jsou ty prvky, které se zobrazí na neutrální prvek. Pokud má jádro právě jeden prvek, je homomorfizmus injektivní.
Prenexní tvar
- Odstranění zbytečných kvantifikátorů5)
- Zbavení se spojek kromě ∧, ∨ a ¬
- Přejmenování proměnných
- Přesun kvantifikátorů doleva (a odstranění neatomických negací)
Metrika
- Musí vždy vyjít kladné číslo.
- Pokud mají 2 body stejné souřadnice, musí vyjít 0.
- Vzdálenost z bodu A do bodu B musí být stejná jako z bodu B do bodu A.
Norma
Značí se ||x||, v podstatě je to dálka vektoru. Euklidovská norma je sqrt(x² + y² + z²).
- Musí vždy vyjít kladné číslo.
- ||x|| = 0, pouze pokud x je nulový vektor.
- ||ax|| = |a| · ||x||
- ||x + y|| ≤ ||x|| + ||y|| (Trojúhelníková nerovnost)
Norma implikuje metriku: |a, b| = ||a − b||
Ortonormalizace
To jako že najdeme bázi jednotkových a kolmých vektorů.
Pokud a * v1 + b * v2 = v3 má řešení, nejsou vektory lineárně nezávislé, tudíž nejsou bázové a nemá to řešení!
Vstupem je nějaká báze (lineárně nezávislé vektory, je jich tolik, jako má prostor dimenzí).
- φ1 = f1 / ||f1||
- hn = fn − (fn · φn−1)6) × φn−1 − (fn · φn−2) × φn−2 − …
- φn = hn / ||hn||
- Opakuj kroky 2 a 3, dokud máš vektory.
Příklad
- f1 = (1, 1, 1)
- f2 = (2, 1, 2)
- f3 = (−1, 0, 1)
- φ1 = f1 / ||f1|| = (1, 1, 1) / sqrt(1² + 1² + 1²) = (1/sqrt(3), 1/sqrt(3), 1/sqrt(3))
- f2 · φ1 = (2, 1, 2) · (1/sqrt(3), 1/sqrt(3), 1/sqrt(3)) = (2/sqrt(3) + 1/sqrt(3) + 2/sqrt(3)) = 5/sqrt(3)
- h2 = f2 − (f2 · φ1) × φ1 = (2, 1, 2) − 5/sqrt(3) × (1/sqrt(3), 1/sqrt(3), 1/sqrt(3)) = (2, 1, 2) − (5/3, 5/3, 5/3) = (1/3, −2/3, 1/3)
- φ2 = (1/3, −2/3, 1/3) / sqrt(2/3) = (1/sqrt(6), −2/sqrt(6), 1/sqrt(6))
- f3 · φ1 = (−1, 0, 1) · (1/sqrt(3), 1/sqrt(3), 1/sqrt(3)) = 0
- f3 · φ2 = (−1, 0, 1) · (1/sqrt(6), −2/sqrt(6), 1/sqrt(6)) = 0
- h3 = f3 − (f3 · φ1) × φ1 − (f3 · φ2) × φ2 = (−1, 0, 1) − 0 × φ1 − 0 × φ2 = (−1, 0, 1)
- φ3 = (−1, 0, 1) / sqrt(2) = (−1/sqrt(2), 0, 1/sqrt(2))
Násobení matic
| a2 | b2 | ||
|---|---|---|---|
| c2 | d2 | ||
| a1 | b1 | a1a2 + b1c2 | a1b2 + b1d2 |
| c1 | d1 | c1a2 + d1c2 | c1b2 + d1d2 |
Grafy
- Suma stupňů všech uzlů = 2 × počet hran
- Grafy jsou izomorfní tehdy, pokud je dokážeš nakreslit jinak, ale přitom je to pořád stejný graf.
- Při reprezentaci grafu maticí bývají řádky odkud a sloupce kam.
- Artikulace je vrchol, který když odstraníme, zvýší se počet komponent.
- Sled je libovolná posloupnost uzlů a hran.
- Tah nesmí opakovat hrany (ale uzly může).
- Cesta nesmí opakovat ani hrany ani uzly.
Nejkratší cesty
- Dijkstra's algorithm – Neumí záporné smyčky.
- Floyd–Warshall algorithm – Když na diagonále vyjde záporné číslo, je tam záporná smyčka. Matici následovníku na začátku vyplníme podle čísla sloupce.
Minimální kostry
- Kruskal's algorithm – Vybírej nejlevnější hrany dokud nemáš pokryté všechny uzly. Nesmí vzniknout kružnice!
- Prim's algorithm – Zvol si uzel, a z něj jdi nejlevnější hranou. Teď máš 2 uzly, zase přidej nejlevnější hranu. Atd. dokud nemáš všechny uzly. Zase bacha na kružnice!