Uživatelské nástroje
Obsah
Numerické metody a matematická pravděpodobnost
Numerické řešení algebraických a obyčejných diferenciálních rovnic
Soustava lineárních rovnic
Jacobi method, Gauss–Seidel method
Jecobiho metoda převede soustavu rovnic do maticového tvaru, upraví ji (
Gauss-Seidelova metoda funguje podobně, jen se výsledek z každého výpočtu (nenásobí se celá matice) hned započítá do dalšího výpočtu. Je tedy rychlejší.
Obě metody konvergují jen tehdy, když je matice soustavy rovnic (ještě před úpravami) ostře diagonálně dominantní. To znamená, že pro každý prvek matice na hlavní diagonále je větší než součet všech zbylých prvků na stejném řádku, a zároveň je větší než součet všech zbylých prvků v témže sloupci.
Jedna nelineární funkce
Půlení intervalů (dřevorubecká metoda)
Newtonova metoda (metoda tečen)
Regula Falsi (metoda sečen)
Diferenciální rovnice
Diferenciální rovnice popisují rozličné (většinou fyzikální) děje. U některých typů rovnic lze nalézt analytické (přesné) řešení. U rovnic složitějších analytické řešení buď neexistuje nebo je obtížné jej nalézt. K tomu se ve výpočetní technice využívá některých numerických metod, která výsledek s určitou přesností aproximuje. Výsledkem výpočtu je například Taylorův rozvoj. Výpočet probíhá iterativně - vždy máme vzorec pro výpočet následujícího členu posloupnosti. Výpočet končí, když je rozdíl dvou následujícíh členů menší než požadovaná přesnost.
Eulerova metoda
 Nejjednodušší metoda – je nutné si pamatovat vzorec! Násleující člen vypočítáme pomocí vzorce
Nejjednodušší metoda – je nutné si pamatovat vzorec! Násleující člen vypočítáme pomocí vzorce
<m>y_{i+1} = y_i + hf(x_i,y_i)</m>
Přesnost Eulerovy metody je rovna velikosti integračního kroku h.
Základní princip je takový, že spočítáme derivaci (směrnici přímky) a s touto směrnicí se pousneme o krok h. Opět spočítáme směrnici, a opět se posuneme… Jak vidno na obrázku, docela to ustřeluje od původní funkce.
Metoda Runge-Kutta
Pokud se mluví o metodě Runge-Kutta, je vetšinou myšlena Runge-Kutta čtvrtého řádu (RK4). K výpočtu následujícího členu je třeba čtyř mezivýpočtů. Tato metoda je daleko rychlejší a přesnější než Eulerova metoda. Rovnice pro výpočet následujícího členu:
<m>k_1 = f(x_n,y_n)</m>
<m>k_2 = f(x_n+1/2h,y_n+1/2hk_1)</m>
<m>k_3 = f(x_n+1/2h,y_n+1/2hk_2)</m>
<m>k_4 = f(x_n+h,y_n+hk_3)</m>
<m>y_{n+1} = y_n+1/6h(k_1+2k_2+2k_3+k_4)</m>
k1 je směrnice na začátku kroku. k2 je směrnice v polovině kroku, s využitím k1 pro výpočet této hodnoty (podobnost s Eulerem není náhodná 
Přesnost RK4 je h5, takže při velikosti kroku 0,1 vznikne chyba řádu 10−5. Abychom dosáhli stejné přesnosti pomocí Eulerovy metody, museli bychom zvolit krok 1000krát menší.
Chyby numerických metod
 Při každé aproximaci musíme počítat s faktorem chyby. Známe chyby dvojího typu – lokální a akumulované. Lokální chyby vznikají v každém kroku a může jít buď o chybu zaokrouhlovací (round-off error) nebo o chybu numerické aproximace (truncation error). Akumulované chyby se sbírají po celou dobu vypočtu.
Při každé aproximaci musíme počítat s faktorem chyby. Známe chyby dvojího typu – lokální a akumulované. Lokální chyby vznikají v každém kroku a může jít buď o chybu zaokrouhlovací (round-off error) nebo o chybu numerické aproximace (truncation error). Akumulované chyby se sbírají po celou dobu vypočtu.
Přesnost výpočtu je závislá na velikosti integračního kroku. Neplatí však, že čím menší krok, tím vyšší přesnost. Při zmenšení kroku pod určitou hodnotu dojde k velkému nárustu chyby numerické aproximace (je to záležitost toho jak počítač reprezentuje data a že bude mít málo platných číslic – viz reprezentace desetinných čísel). Obrázek ilustuje hledaní ideální délky kroku.
Vícekrokové numerické metody
K výpočtu následujícího členu je využito předchozích výsledků. Jejich slabina spočívá v pomalém „rozjezdu“. Pokud je pro výpočet třeba např. čtyř předchozích členů, musíme je na začátku aproximace spočítat jedou z jednokrokových metod, většinou RK4. Vícekrokové metody přestávají být efektivní ve chvílí, kdy je funkce nespojitá. Při nespojitostech je třeba opětovného hledání prvních bodů a to metodu brzdí. Příkladem vícekroké metody je Adams-Bashforth (vzorec jenom pro zajímavost, to snad není třeba vědět).
<m>y_{n+1} = y_n + h/24(55f_n - 59f_{n-1} + 37f_{n-2} - 9f_{n-3})</m>
Rozložení pravděpodobnosti
Probability distribution, Cumulative distribution function
Označení f(x) je používáno pro hustotu rozdělení pravděpodobnosti, F(X) slouží pro označení distribuční funkce. Pokud vypočítáme integrál funkce hustoty v intervalu (x1, x2), získáme pravděpodobnost, že náhodná veličina X bude mít hodnotu z tohoto intervalu. Distribuční funkce je neklesající a zprava spojitá. V každém bodě vyjadřuje její funkční hodnota pravděpodobnost, že náhodná veličina X nabyde hodnoty menší nebo rovné tomuto bodu.

Rovnoměrné rozložení
Uniform distribution (continuous)
Obvykle označujeme R(a,b), kde a je nejmenší možná hodnota náhodné proměnné X, b je největší. V normálové formě R(0,1) je základem pro generování dalších rozložení.
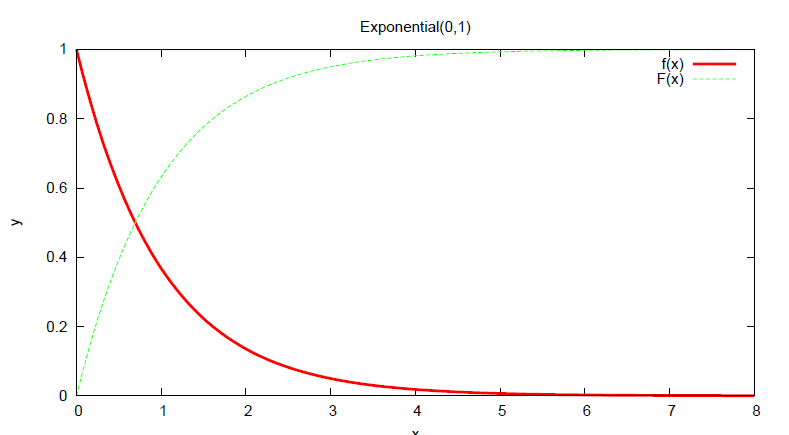
Exponenciální rozložení
Používá se pro reprezentaci rozložení doby obsluhy zařízení, časových intervalů mezi poruchmi, mezi příchody požadavků… První parametr je počáteční hodnota, druhý je součástí vzorce pro funkci hustoty (snad nemusíme umět, moc se to nebralo).
Normální (Gausovo) rozložení
Odpovídá jevům s vlivem většího počtu nezávislých faktorů. První parametr je střed, tzn. bod, ve kterém je hustota největší. Druhý parametr určuje v podstatě výšku tohoto bodu (opět přes funkci hustoty).
Pearsonovo rozložení
Celým názvem Pearsonovo rozložení χ21). Používá se při testování statistických hypotéz.
Generování pseudonáhodných čísel
Základem je kvalitní generátor rovnoměrného rozložení. Transformací rovnoměrného rozložení zísáme soubor čísel jiného rozložení. Řešíme problém mezí náhodností a pseudonáhodností. Pomocí počítače lze generovat i náhodná čísla, ale potřebujeme k tomu například speciální hardware, protože počítač (procesor) je deterministický stroj, takže čísla, která generuje, jsou též deterministická. Charakteristika pseudonáhodných čísel je taková, že pro stejný základ je přístí generované číslo stejné. Generování náhodných čísel je navíc pomalé. Algoritmické generátory generují pseudonáhodná čísla daleko vyšší rychlostí.
Kongruentní generátory
Pro generování čísel používají vztah
<m>x_{n+1} = (ax_n + b) mod m</m>
kde konstanty a, b a m musí mít vhodné hodnoty – hlavně musí být nesoudělné! Obvykle se užívá vyšších prvočísel. Generují rovnoměrné rozložení. Výsledkem je konečná posloupnost – po určitém počtu vygenerovaných hodnot se začne opakovat (perioda generátoru).
Shrnutí (osnova)
Numerické metody
- soustava lineárních algebraických rovnic: jacobiho metoda, gauss seidler
- jedna algebraická nelineární: půlení intervalu, regula falsi, sečny, tečny (konvergence)
- jednoduchá diferenciální (složité se dají převést): eulerova metoda, runge-kutta
Pravděpodobnost
- rozložení definováno hustotou, distribuční funkce
- normální, exponenciální, rovnoměrné, hrušky syn
- náhodné vs pseudonáhodné
- kongruentní generátor
- převod do rozdělení pravděpodobnosti: inverzní distribuční funkce, monte carlo?