Uživatelské nástroje
Úkol 1
Bc. Jan Kaláb <[email protected]>
Příklad 1
Uvažte jazyk L1 = {aibjci+j | i ≥ 0, j ≥ 0}.
Sestavte gramatiku G1 takovou, že L(G1) = L1.
G1 = ({a, b, c}, {S, A, B}, S, P)
P = {
- S → A
- A → aAc | B
- B → bBc | ε
}
Jakého typu (dle Chomského hierarchie jazyků) je G1 a jakého typu je L1? Mohou se tyto typy obecně lišit? Svoje tvrzení zdůvodněte.
G1 i L1 jsou bezkontextové. G1 má pravidla ve tvaru „neterminál → posloupnost terminálů a neterminálů“. L1 lze reprezentovat zásobníkovým automatem (ale ne konečným automatem).
Obecně se lišit mohou. Chomského hierarchie jazyků a gramatik má strukturu „vrstev“ – bezkontextové gramatiky lze popsat i jako kontextové či obecné, ale ne jako regulární. To samé platí i pro jazyky. Důsledkem je, že bezkontextový jazyk jistě půjde popsat kontextovou gramatikou.
Příklad 2
Uvažte regulární výraz r2 = (ab + abc)* ab*.
Převeďte r2 algoritmicky na minimální deterministický konečný automat M2 (tj. RV → RKA → DKA → minimální DKA), přijímající jazyk popsaný výrazem r2.
Úplně definovaný DKA:
| a | b | c | |
|---|---|---|---|
| →ε-uz({1}) = {1, 2, 3, 6, 11} = A | ε-uz({4, 7, 12}) = {4, 7, 12, 13, 15} = B | ε-uz({}) = ∅ = T | ε-uz({}) = ∅ = T |
| ←B | ε-uz({}) = ∅ = T | ε-uz({5, 8, 14}) = {2, 3, 5, 6, 8, 10, 11, 13, 14, 15} = C | ε-uz({}) = ∅ = T |
| ←C | ε-uz({4, 7, 12}) = {4, 7, 12, 13, 15} = B | ε-uz({14}) = {13, 14, 15} = D | ε-uz({9}) = {2, 3, 6, 9, 10, 11} = E |
| ←D | ε-uz({}) = ∅ = T | ε-uz({14}) = {13, 14, 15} = D | ε-uz({}) = ∅ = T |
| E | ε-uz({4, 7, 12}) = {4, 7, 12, 13, 15} = B | ε-uz({}) = ∅ = T | ε-uz({}) = ∅ = T |
| T | T | T | T |
Minimalizace:
| ≡0 | a | b | c | ||||
|---|---|---|---|---|---|---|---|
| ←I | ←B | T | II | C | I | T | II |
| ←D | |||||||
| ←C | B | I | D | I | E | II | |
| →II | →A | B | I | T | II | T | II |
| E | |||||||
| T | T | II | T | II | T | II | |
| ≡1 | a | b | c | ||||
|---|---|---|---|---|---|---|---|
| ←I | ←B | T | IV | C | II | T | IV |
| ←D | T | IV | D | I | T | IV | |
| ←II | ←C | B | I | D | I | E | III |
| →III | →A | B | I | T | IV | T | IV |
| E | |||||||
| IV | T | T | IV | T | IV | T | IV |
| ≡2 | a | b | c | ||||
|---|---|---|---|---|---|---|---|
| ←I | ←B | T | V | C | III | T | V |
| ←II | ←D | T | V | D | II | T | V |
| ←III | ←C | B | I | D | II | E | IV |
| →IV | →A | B | I | T | V | T | V |
| E | |||||||
| V | T | T | V | T | IV | T | IV |
≡2 = ≡3 = ≡
Převeďte automat M2 na minimální deterministický konečný automat M2′ přijímající komplement jazyka (nad abecedou {a, b, c}) popsaného výrazem r2.
Příklad 3
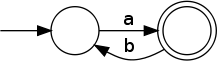
Uvažte NKA M3 nad abecedou Σ = {a, b} z obrázku 1:

Řešením rovnic nad regulárními výrazy sestavte k tomuto automatu ekvivalentní regulární výraz.
Pozn.: Stavy jsem si označil X, Y, Z ve směru z leva.
- X = aY + aZ + ε
- Y = aY + bZ
- Z = aZ + bX
- X = aY + aZ + ε
- Y = a*bZ
- Z = a*bX
- X = aa*bZ + aa*bX + ε
- X = aa*ba*bX + aa*bX + ε
- X = (aa*ba*b + aa*b)X + ε
- X = (aa*ba*b + aa*b)*ε
(a+ba*b + a+b)*
Příklad 4
Mějme operaci even : Σ* → Σ*, která z daného slova w ∈ Σ* vybere pouze znaky na sudých pozicích. Například: even(abcda) = bd, even(aabbcc) = abc.
Navrhněte a formálně popište algoritmus, který má na vstupu nedeterministický konečný automat M1, a jehož výstupem bude automat M2 takový, že L(M2) = {even(w) | w ∈ L(M1)}.
Vstup: NKA M1 = (Q1, Σ1, δ1, q01, F1)
Výstup: M2 = (Q2, Σ2, δ2, q02, F2)
- Q2 ⊆ Q1
- Σ2 ⊆ Σ1
-
- ∀q11, q21, q31 ∈ Q1
∀q12, q22 ∈ Q2
∀a, b ∈ Σ1 ∧ ∀b ∈ Σ2:
q22 ∈ δ2(q12, b) ⇔ (δ1(q11, a) = q21 ∧ δ1(q21, b) = q31) - ∀q11, q21 ∈ Q1 ∧ q21 ∈ F1
∀q12, q22 ∈ Q2
∀a ∈ Σ1:
q22 ∈ δ2(q12, ε) ⇔ (δ1(q11, a) = q21 ∧ δ1(q21, ε) = q21)
- q01 = q02
- F2 = F1
Příklad 5
Mějme jazyk L = {aibja2i | 0 ≤ i, 0 ≤ j ≤ 5}. Je jazyk L regulární? Dokažte nebo vyvraťte.
Lemma
Nechť L je regulární jazyk. Pak existuje n ∈ N takové, že libovolné slovo w ∈ L délky alespoň n lze psát ve tvaru w = xyz, kde |xy| ≤ n, y ≠ ε a xyiz ∈ L pro každé i ∈ N0.
Řešení
Budeme provádět důkaz sporem. Předpokládejme, že L je regulární.
Z uvedené pumping lemmy a z předpokladu plyne, že musí existovat konstanta n.
Uvažujme libovolnou hodnotu n.
Pro w = anb4a2n náležící L, platí |w| ≥ n.
Uvažujme libovolný výběr x, y, z takový, že w = xyz ∧ |xy| ≤ n ∧ y ≠ ε.
Uvažujme například rozdělení:
- x = am
- y = an−m
- z = b4a2n
Pro i = 2 platí: xyiz = a2n−mb4a2n ∉ L protože, 2n − m ≠ 2n.
Obdobně lze dokázat pro libovolná jiná rozdělení w = xyz se stejnou pumpovací konstantou i = 2.
Dochází ke sporu, protože w po pumpování nenáleží do jazyka L a tedy L není regulární.
Příklad 6
Uvažujme algebru regulárních množin (ARM) nad abecedou Σ.
Ukažte, že pro ARM platí následující teorém Kleeneho algebry: a(ba)* = (ab)*a.
Výše uvedený konečný automat je minimální konečný automat který přijímá i zamítá stejné řetězce jako regulární výraz na levé i pravé straně teorému. Proto je teorém platný.
Vzhledem k uspořádání definovaném v Kleeneho algebře určete, zdali je {ε} minimálním prvkem ARM. Své tvrzení dokažte.
Předpokládejme, že {ε} je minimálním prvkem ARM. Pak by vzhledem k uspořádání definovaném v Kleeneho algebře muselo platit: {ε} ∪ {a} = {a}. Ovšem {ε} ∪ {a} = {ε, a}. Dochází tedy ke sporu, tedy {ε} není minimálním prvkem ARM.