Uživatelské nástroje
Obsah
Úkol 2
Bc. Jan Kaláb <[email protected]>
Příklad 1
Navrhněte algoritmus, který pro daný netereminál A a bezkontextovou gramatiku G = (N, Σ, P, S) rozhodne, zda A je prvním symbolem nějaké větné formy G, t.j., zda S ⇒* Aγ, kde γ ∈ (Σ ∪ N)*. Uvědomte si, že některé neterminály mohou být přepsány na ε.
Vstup: G = (N, Σ, P, S); A ∈ N
Výstup: Boolean (✔✘)
- A = S: ✔
- Sestrojíme množinu E, která bude obsahovat neterminály, které se přímo přepisují na ε.
- Hledáme v P pravidla tvaru X → E* a všechna taková X přidáme do E. Opakujeme, dokud se E mění.
- Hledáme v P pravidla tvaru X → E*A(N ∪ Σ)* a ze všch takových X uděláme množinu T. Tanto krok opakujeme, ale místo A dosazujeme neterminály z T, a stále rozšiřujeme množinu T, dokud můžeme.
- Množina T obsahuje počáteční symbol S. ✔
- ✘
Příklad 2
Nalezněte bezkontextovou gramatiku G s co nejméně pravidly takovou, že pokud v algoritmu 4.3 z přednášky pro odstranění zbytečných symbolů nejdříve provedeme body 3 a 4 (algoritmus 4.2 aplikujeme přímo na G a odstraníme nedostupné symboly) a na výslednou gramatiku aplikujeme body 1 a 2 (odstraníme neterminály jež negenerují žádné věty), dostaneme gramatiku obsahující nedostupný symbol.
G = ({A, B, C}, {a, b, c}, P, A)
- A → BC | a
- B → b
- C → cC
Příklad 3
Gramatiku G = ({A, B, C}, (a, b, c}, P, A) s pravidly
- A → Ba | a
- B → BbC | C
- C → Cc | A
převeďte algoritmicky do Greibachové normální formy a Chomského normální formy.
Greibachové normální forma
- Ostranění ε-pravidel: žádné nejsou.
- Odstranění levé rekurze:
- A → a | aA′
- A′ → a | C′a | B′a | C′B′a | aA′ | C′aA′ | B′aA′ | C′B′aA′
- B → C | CB′
- B′ → bC | bCB′
- C → A | AC′
- C′ → c | cC′
- Relace uspořádání: A′ < C′ < B′ < B < C < A
- Dosazení v pořadí inverzním k relaci uspořádání:
- A → a | aA′
- C → a | aA′ | aC′ | aA′C′
- B → a | aA′ | aC′ | aA′C′ | aB′ | aA′B′ | aC′B′ | aA′C′B′
- B′ → bC | bCB′
- C′ → c | cC′
- A′ → a | ca | cC′a | bCa | bCB′a | cB′a | cC′B′a | aA′ | caA′ | cC′aA′ | bCaA′ | bCB′aA′ | cB′aA′ | cC′B′aA′
- Upravíme pravidla do greibachové normální formy:
- A → a | aA′
- C → a | aA′ | aC′ | aA′C′
- B → a | aA′ | aC′ | aA′C′ | aB′ | aA′B′ | aC′B′ | aA′C′B′
- B′ → bC | bCB′
- C′ → c | cC′
- A′ → a | cA″ | cC′A″ | bCA″ | bCB′A″ | cB′A″ | cC′B′A″ | aA′ | cA″A′ | cC′A″A′ | bCA″A′ | bCB′A″A′ | cB′A″A′ | cC′B′A″A′
- A″ → a
Chomského normální forma
- Vlastní gramatika: zadaná gramatika už vlastní je.
- Bez jednoduchých pravidel:
- NA = {A}
- NB = {A, B, C}
- NC = {A, C}
- A → Ba | a
- B → BbC | Cc | Ba | a
- C → Cc | Ba | a
- Chomského normální forma
- A → Ba′ | a
- B → B<bc> | Cc′ | Ba′ | a
- C → Cc′ | Ba′ | a
- a′ → a
- c′ → c
- <bc> → b′C
- b′ → b
Příklad 4
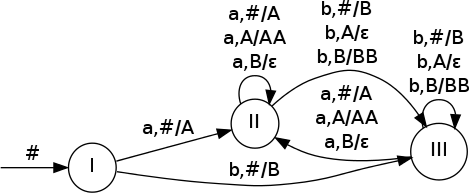
Navrhněte deterministický zásobníkový automat přijímající jazyk L z příkladu 6. Přechodovou funkci znázorněte graficky. Automat může mít maximálně 4 zásobníkové symboly a 4 stavy. Demonstrujte přijetí slova abba.
M = ({I, II, III}, {a, b}, {A, B, #}, δ, I, #, {})
| Čtený symbol | Zásobník1) | Přechodová funkce |
|---|---|---|
| # | ||
| a | #A | 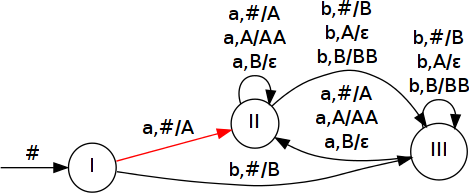 |
| b | # |  |
| b | #B | 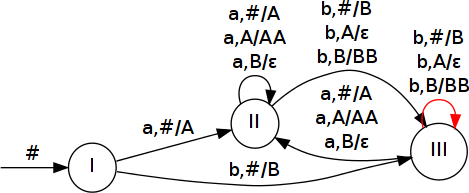 |
| a | # | 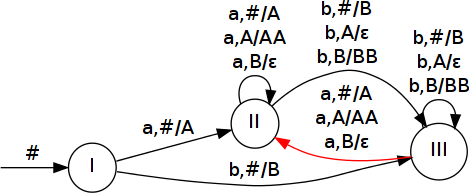 |
Příklad 5
Operátor paralelní kompozice (tzv. shuffle) || : Σ* × Σ* → 2Σ* je definován induktivně tak, že w || ε = ε || w = {w} a aw1 || bw2 = {a} · (w1 || bw2) ∪ {b} · (aw1 || w2). Dále, pro jazyky L1 a L2, L1 || L2 = ∪w1 ∈ L1, w2 ∈ L2. Například {aa}||{bb} = {aabb, abab, abba, baab, baba, bbaa}. Dokažte, že množina bezkontextových jazyků není uzavřena na ||. Postupujte podobně, jako v důkazu neuzavřenosti vůči průniku, t.j., zvolte si dva bezkontextové jazyky L1, L2 a dokažte pomocí pumping lemmatu, že L1 || L2 není bezkontextový.
- L1 = {anbn | n ≥ 0}
- L2 = {0m1m | m ≥ 0}
- L = L1 || L2 = {w | #a = #b ∧ #0 = #1}
Předpokládejme, že L je bezkontextový jazyk.
- ∀ k: z ∈ L ∧ |z| ≥ k
- z = ak0kbk1k, |z| = 4k ≥ k
- ∀ uvwxy, vx ≠ ε, |vwx| ≤ k
- i = 2
Takto mohou vzniknout řetězce ve tvaru aa…aa00…00bb…bb11…11. Počet opakování jednotlivých symbolů bude k, a pak pro libovolný výběr vwx takový, že |vwx| ≤ k a „napumpování“ dojde vždy k narušení stejného počtu symbolů.
Z výše uvedeného tvrzení plyne, že jazyk L není bezkontextový, a tudíž množina bezkontextových jazyků není uavřena na ||.
Příklad 6
Nechť L je jazyk všech slov nad abecedou {a, b} se stejným počtem výskytů symbolu a jako výskytů symbolu b. Mějme gramatiku G = (S, {a, b}, P, S) s pravidly
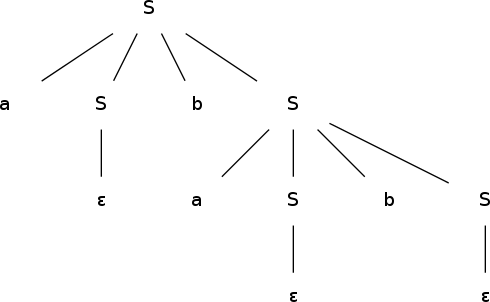
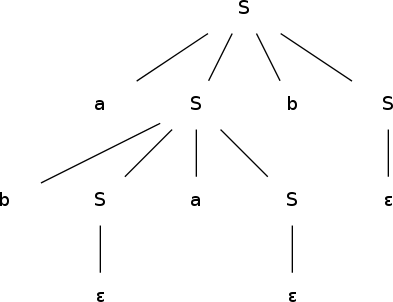
- S → aSbS | bSaS | ε
Je gramatika jednoznačná? Dokažte.
Dokažte indukcí k délce slova, že L(G) ⊆ L.
- ∀ w ∈ L(G): |w| = 0 → w ∈ L
- i = 2
Z jazyka L můžeme udělat pouze tyto řetězce délky i: ab, ba. Zcela stejn řetězce můžeme vygenerovat i z jazyka L(G) a také to budou jediné možné řetězce o délce i, protože gramatika G vždy generuje stejný počet symbolů a jako b. - Výše uvedené tvrzení platí i pro všechna následující i + 2. (Vygenerované řetězce budou samozřejmě odpovídat patřičné délce i.)
Nechť pro i ∈ ℕ, Li = {w ∈ L | |w| ≤ i}. Dokažte indukcí k i, že Li ⊆ L(G) pro všechna i ∈ ℕ (a tedy L ⊆ L(G)).
Nápověda:
- Nejprve zdůvodněte následující tvrzení: Nechť slovo w ∈ L \ {ε} má tu vlastnost, že žádný jeho vlastní prefix vyjma ε nepatří do L. Potom w je tvaru aub, nebo bua, kde u ∈ L.
- Pomocí tvrzení z bodu 1. ukažte, že každé slovo w ∈ L \ {ε} lze napsat ve tvaru aubv, nebo buav, kde u, v ∈ L.
- Tvrzení z bodu 2. použijte v indukčním kroce.